プログラミング

公開日：2020/03/05 最終更新日：2021/08/16

GAN (Generative Adversarial Network) の理論と実装

ディープラーニングを活用した生成モデルの中でも、最も応用手法が研究されている GAN (Generative Adversarial Network) ですが、「２つのネットワークを互いに競わせるように学習する」アーキテクチャであるということはご存知の方も多いでしょう（下図）。

しかし、その一方で、なぜそれによって適切にデータが生成されるのかについては、きちんと説明がなされている情報をあまり目にする機会もなく、それゆえに、きちんと説明できる方も少ないのではないでしょうか。

そこで、本記事では、GAN の理論的な部分の説明を、きちんと数式を混じえつつ書き進めていきたいと思います。その後、PyTorch を用いた実装も紹介していきます。

1 生成モデルの目的
2 GAN における識別器の定式化
3 GAN における生成器の定式化
4 GAN 全体の定式化
- 4.1 識別器の学習
- 4.2 生成器の学習
5 GAN の実装

生成モデルの目的

そもそも、生成モデルの目的は何だったでしょうか？識別モデルにおいては、予測値と実際の値が一致すればよいという、至極当然な目標がありましたが（実際にはデータを適切に分類する決定境界を見つける）、生成モデルでは「正解となる出力値」はありません。

では何をすべきなのかと言うと、「データに近いモデル分布を見つける」ことになります。すなわち、生成モデルでは、「今観測できているデータは、なんらかの確率分布に基づいて生成されているはずだ」という考えに基づいて、そのデータを生成している確率分布そのものをモデル化しようと試みていることになります。

よって、データ分布とモデル分布という、２つの確率分布の「距離」を近づけることが目指すべきことになります。以下、確率変数\(x\)に対し、データ分布を\(p_d(x)\)、モデル分布を\(p_g(x)\)で表すことにします。

GAN における識別器の定式化

GAN においてもデータ分布に近いモデル分布を求めたいわけですが、実際に分布\(p_d(x)\)を求めることを考えた場合、少し困ったことが起こります。

というのも、分布\(p_d(x)\)は分布の形が明示されているわけではないので、どのような形かはわからないのです。そのため、直接尤度を計算する（ことによってデータ分布との近さを測る）といったことができません。

そこで、まずは直接尤度を測る代わりに、データ分布とモデル分布の密度比\(r(x)\)を考えます。

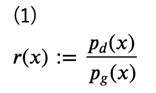
ここで、データ分布あるいはモデル分布から生成されたラベル付きのデータ集合\(\left\{ (x_1, y_1), \cdots, (x_N, y_N)\right\}\)を考え、データ分布により生成されたデータのラベルを\( y=1\)、モデル分布により生成されたデータのラベルを\( y=0\)とすると、それぞれの分布は次のように表されます。

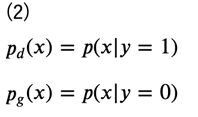
このとき、密度比\(r(x)\)の式は次のように変形することができます。

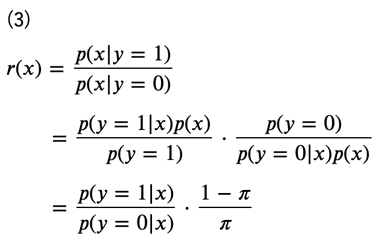
ただし、

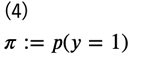
としています。この\(\pi\)は実際のデータ数の比で近似することができるので、ラベルが\(y=0\)あるいは\(y=1\)のみであることを考えると、\(p(y=1∣x)\)を推定することができれば、密度比\(r(x)\)が求まることになります。そこで、この\(p(y=1∣x)\)を近似する分布をパラメータ\(\phi\)を用いて\(q_\phi(y=1∣x)\)とします。

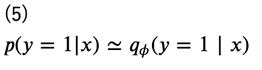
こうすることで、この分布を（例えば）ニューラルネットワークで求めることができるようになります。この\(q_\phi(y=1∣x)\)を推定するモデルのことを識別器あるいは鑑別器 (discriminator) と言います。識別器を\(D(\phi;x)\)で表しておきます。

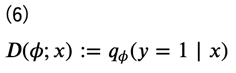
これにより、元々は密度比を考える問題であったものが、確率的分類器の最適化、すなわち一般的な分類問題に置き換わったことになります。よって、誤差関数として交差エントロピー誤差関数\(U(D)\)を考えると、次のように表すことができます。

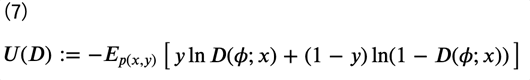
ただし、\(E\begin{bmatrix}⋅\end{bmatrix}\)は期待値を表します。符号の煩わしさから、\(−U(D) \)を考え、次のように式変形をします。

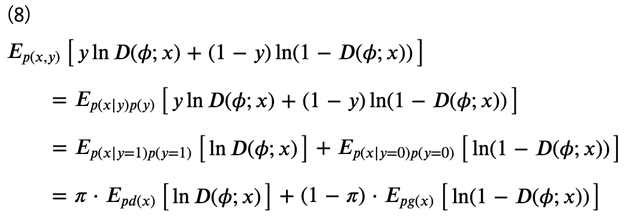
ここで、データ集合に関して、各ラベルのデータが半々、すなわち\(y=0\)と\(y=1\)のデータ数が等しかったとすると、

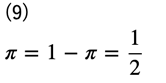
となるため、式(8)より、最終的な識別器の目的関数\(V(D)\)は次のように表すことができます。

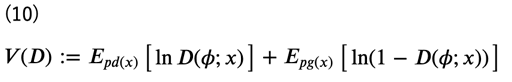
識別器の目的はこれを最大化することになります。

GAN における生成器の定式化

生成器について見ていく前に、先ほどの\(V(D)\)に関してもう少し考えてみましょう。もし最適な識別器\(D^{∗}(\phi;x)\)が得られたとすると、

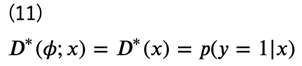
となりますが、このとき、\(D^{∗}(x)\)は

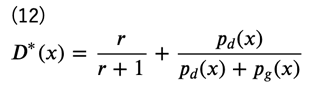
に収束します。これを式(10)に代入すると、次のようになります（ただし、見やすさのため、\(p_d(x),p_g(x)\)をそれぞれ\(p_d,p_g\)で表しています）。

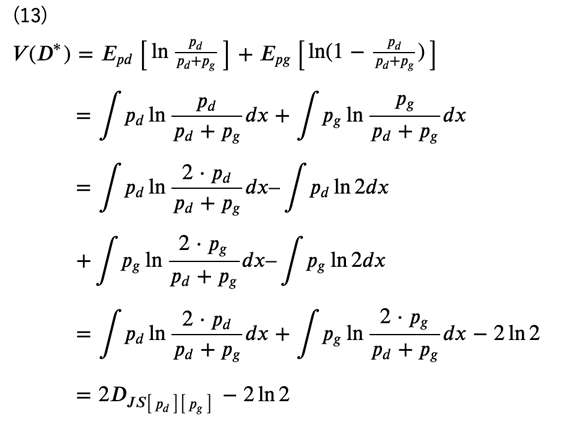
ただし、最後の\(D_{JS}\begin{bmatrix}⋅\end{bmatrix}\)はJSダイバージェンス / イェンゼン・シャノン情報量 (Jensen-Shannon divergence) を表しています。すなわち、\(V(D^*)\)は\(p_d(x)\)と\(p_g(x)\)のJSダイバージェンスに対応していることが分かります。本来の生成モデルの目的はデータ分布に近いモデル分布を求めることでしたので、学習によって得られた識別器\((D^*(x))\)を用いれば、生成モデルに対しても同じ目的関数を用いることができそうです。

では、モデル分布（生成モデル）について考えていきましょう。ここで、潜在変数\(z\)を仮定します。すると、周辺化により

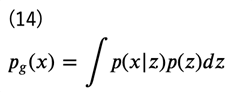
となりますが、今度は\( p(x|z)\)を近似する分布として\(q_\theta (x|z) \)を導入します。

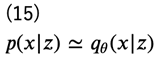
こうすることで、再度この分布を（例えば）ニューラルネットワークで求めることができるようになります。\(q_\theta (x|z)\)を推定するモデルのことを、識別器に対して 生成器 (generator) と言います。生成器を\(G(\theta;z)\)で表しておきます。

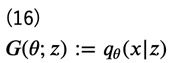
式(13) で示した通り、\(V(D^*)\)は\(p_d(x)\)と\(p_g(x)\)のJSダイバージェンスに対応していますので、最適な\(G(\theta;z)\)を得るための目的関数は次のように書くことができます。

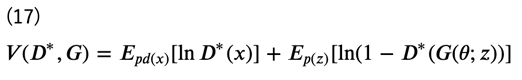
ただし、識別器は \(V(D)\)を最大化することが目的でしたが、生成器はこの\(V(D^*,G)\)を最小化することが目的であることに注意が必要です。

GAN 全体の定式化

さて、識別器・生成器の定式化を考えた際、いずれの分布についても、「（例えば）ニューラルネットワークで求めることができる」と敢えて書きました。実は、GANのアーキテクチャ自体は、モデルに関してはニューラルネットワークにしなくてはならないわけではありません。ただし、実際は識別器・生成器ともに（ディープ）ニューラルネットワークで表現した手法が用いられています。

それぞれの目的関数は式(10)および式(17)で示した通りですが、実際に最適化を考えると、適切な生成器が得られないと最適な識別器は学習できませんし、反対に適切な識別器が得られないと最適な生成器を学習することはできません。よって、学習ではそれぞれの目的関数を交互に最適化することになります。式で表してみると、次の通りです。

識別器の学習

生成器\(G(\theta;z)\)は固定した上で、以下の式を計算する。

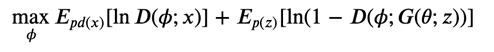
生成器の学習

生成器\(D(\phi;x)\)は固定した上で、以下の式を計算する。

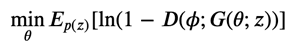
これが、いわゆる「２つのネットワークを互いに競わせるように学習する」で知られる GAN の正体なわけです。識別器・生成器の学習の式をまとめて考えると、簡易的には次の式を考えているとも言えるでしょう。

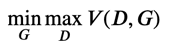
学習が十分に進むと、生成器\(G(\theta;z)\)から生成されるデータは、実際のデータに非常に近いものとなります。

GAN の実装

では、GANの実装を考えていきましょう。モデル定式化の過程は複雑でしたが、実装はシンプルにまとまります。データは FashionMNIST を用いることにしましょう。まずは用いるライブラリについてです。

import os
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizers
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import torchvision
import torchvision.transforms as transforms
import matplotlib
# matplotlib.use('Agg')
import matplotlib.pyplot as plt

コメントアウトしてある matplotlib.use(‘Agg’) は、実行している環境によっては必要になります（グラフの可視化用）。

はじめに、モデルの定義 GAN クラスを実装します。ただし、これはあくまでも “GAN” という名前でまとめるために実装したクラスであり、大事になるのはこの後実装していく識別器 Discriminator および生成器 Generator になります。forward も実装はしていますが、実際に用いることはありません。

class GAN(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.G = Generator(device=device)
self.D = Discriminator(device=device)

def forward(self, x):
x = self.G(x)
y = self.D(x)

return y

続いて、識別器\(D\)の実装です。今回用いるのは画像データですので、ネットワークとしてCNNを実装します（ネットワーク構造の詳細については割愛します）。出力は生成された画像が本物か偽物かの判別（２クラス分類）ですので、出力層の活性化関数はsigmoid関数となります。

class Discriminator(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.conv1 = nn.Conv2d(1, 128,
kernel_size=(3, 3),
stride=(2, 2),
padding=1)
self.relu1 = nn.LeakyReLU(0.2)
self.conv2 = nn.Conv2d(128, 256,
kernel_size=(3, 3),
stride=(2, 2),
padding=1)
self.bn2 = nn.BatchNorm2d(256)
self.relu2 = nn.LeakyReLU(0.2)
self.fc = nn.Linear(256*7*7, 1024)
self.bn3 = nn.BatchNorm1d(1024)
self.relu3 = nn.LeakyReLU(0.2)
self.out = nn.Linear(1024, 1)

def forward(self, x):
h = self.conv1(x)
h = self.relu1(h)
h = self.conv2(h)
h = self.bn2(h)
h = self.relu2(h)
h = h.view(-1, 256*7*7)
h = self.fc(h)
h = self.bn3(h)
h = self.relu3(h)
h = self.out(h)
y = torch.sigmoid(h)

return y

生成器 \(G\)の実装は次の通りです。入力としてノイズを受け取った後、途中 F.interpolate では出力サイズを合わせるため、Upsamplingをしています。

class Generator(nn.Module):
def __init__(self,
input_dim=100,
device='cpu'):
super().__init__()
self.device = device
self.linear = nn.Linear(input_dim, 256*14*14)
self.bn1 = nn.BatchNorm1d(256*14*14)
self.relu1 = nn.ReLU()
self.conv1 = nn.Conv2d(256, 128,
kernel_size=(3, 3),
padding=1)
self.bn2 = nn.BatchNorm2d(128)
self.relu2 = nn.ReLU()
self.conv2 = nn.Conv2d(128, 64,
kernel_size=(3, 3),
padding=1)
self.bn3 = nn.BatchNorm2d(64)
self.relu3 = nn.ReLU()
self.conv3 = nn.Conv2d(64, 1,
kernel_size=(1, 1))

def forward(self, x):
h = self.linear(x)
h = self.bn1(h)
h = self.relu1(h)
h = h.view(-1, 256, 14, 14)
h = F.interpolate(h, size=(28, 28))
h = self.conv1(h)
h = self.bn2(h)
h = self.relu2(h)
h = self.conv2(h)
h = self.bn3(h)
h = self.relu3(h)
h = self.conv3(h)
y = torch.sigmoid(h)

return y

これでモデルの実際ができました。GAN は学習の枠組みのことを指していますので、\(D\)にせよ、\(G\)にせよ、ネットワーク自体に大きな特徴はありません。では、学習・生成を行っていきましょう。

if __name__ == '__main__':
np.random.seed(1234)
torch.manual_seed(1234)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

'''
1. データの読み込み
'''
# TODO

'''
2. モデルの構築
'''
# TODO

'''
3. モデルの訓練
'''
# TODO

'''
4. モデルの評価
'''
# TODO

1. データの読み込み

torchvision を用いて FashionMNIST データを読み込みます。

'''
1. データの読み込み
'''
root = os.path.join(os.path.dirname(__file__),
'.', 'data', 'fashion_mnist')
transform = transforms.Compose([transforms.ToTensor(),
lambda x: x.view(-1)])
mnist_train = \
torchvision.datasets.FashionMNIST(root=root,
download=True,
train=True,
transform=transform)
train_dataloader = DataLoader(mnist_train,
batch_size=100,
shuffle=True)

Jupyter Notebook で実行する場合、上記の os.path.dirname(__file__) はエラーになりますので注意してください（データを保存したいパスをそのまま記述してください）。

2. モデルの構築

GAN クラスのインスタンスを生成します。また、GAN では、生成器\(G\)に与える潜在変数\(z\)は分布を明示しませんので、ノイズとして一様乱数を用いることにし、ノイズを生成する関数を gen_noise として実装しておきます。

'''
2. モデルの構築
'''
model = GAN(device=device).to(device)

def gen_noise(batch_size):
return torch.empty(batch_size, 100).uniform_(0, 1).to(device)

3. モデルの訓練

GAN は\(D\)と\(G\)をそれぞれ交互に最適化していきますので、オプティマイザもそれぞれに用意します。ともに手法としてはAdamを用いていますが、GANの学習のテクニックとして、初期の学習率を小さめに設定しています。また、誤差関数は２クラス版の交差エントロピー誤差関数を用います。実際の学習部分を実装する train_step は、また後ほど見ていくことにしましょう。

'''
3. モデルの訓練
'''
criterion = nn.BCELoss()
optimizer_D = optimizers.Adam(model.D.parameters(), lr=0.0002)
optimizer_G = optimizers.Adam(model.G.parameters(), lr=0.0002)

def compute_loss(label, preds):
return criterion(preds, label)

def train_step(x):
batch_size = x.size(0)
model.D.train()
model.G.train()

# 識別器の訓練
# TODO

# 生成器の訓練
# TODO

return loss_D, loss_G

識別器の訓練

識別器 \(D\)では、本物画像と偽物画像を正しく識別できることを目的としますので、それぞれの画像を入力して得られた予測結果と、それぞれに対するラベル（本物画像が\(t=1\)、偽物画像が \(t=0\))を元に、誤差関数の最小化を行います。

# 識別器の訓練
# 本物画像
preds = model.D(x).squeeze() # 本物画像に対する予測
t = torch.ones(batch_size).float().to(device)
loss_D_real = compute_loss(t, preds)
# 偽物画像
noise = gen_noise(batch_size)
gen = model.G(noise)
preds = model.D(gen.detach()).squeeze() # 偽物画像に対する予測
t = torch.zeros(batch_size).float().to(device)
loss_D_fake = compute_loss(t, preds)

loss_D = loss_D_real + loss_D_fake
optimizer_D.zero_grad()
loss_D.backward()
optimizer_D.step()

注意すべきは、偽物画像を用いる際、生成器\(G\)に勾配が伝わらないようにするために、.detach() を用いる必要があるということでしょう。

gen = model.G(noise)
preds = model.D(gen.detach()).squeeze()

生成器の訓練

生成器\(G\)では、生成した画像データを識別器\(D\)が「本物」と間違えるように学習をしたいので、生成画像（偽物画像）のラベルを本物\((t=1) \)として学習するのがポイントです。

# 生成器の訓練
noise = gen_noise(batch_size)
gen = model.G(noise)
preds = model.D(gen).squeeze() # 偽物画像に対する予測
t = torch.ones(batch_size).float().to(device) # 偽物画像のラベルを「本物画像」に
loss_G = compute_loss(t, preds)
optimizer_G.zero_grad()
loss_G.backward()
optimizer_G.step()

これで train_step が実装できたので、実際に学習をしてみます。

epochs = 20

for epoch in range(epochs):
train_loss_D = 0.
train_loss_G = 0.
test_loss = 0.

for (x, _) in train_dataloader:
x = x.to(device)
loss_D, loss_G = train_step(x)

train_loss_D += loss_D.item()
train_loss_G += loss_G.item()

train_loss_D /= len(train_dataloader)
train_loss_G /= len(train_dataloader)

print('Epoch: {}, D Cost: {:.3f}, G Cost: {:.3f}'.format(
epoch+1,
train_loss_D,
train_loss_G
))

実行すると、次のような結果が得られます。

Epoch: 1, D Cost: 0.630, G Cost: 1.582
Epoch: 2, D Cost: 0.422, G Cost: 2.139
Epoch: 3, D Cost: 0.435, G Cost: 2.199
...
Epoch: 18, D Cost: 0.289, G Cost: 3.350
Epoch: 19, D Cost: 0.272, G Cost: 3.389
Epoch: 20, D Cost: 0.279, G Cost: 3.444

今回は\(D\)の誤差が減少し続け、\(G\)の誤差が増加し続けるという結果となりましたが、GAN は \(D\)と\(G\)が競い合って学習をするという性質上、お互いの誤差が増減し合って学習が進むといったこともよく起こります。

4. モデルの評価

学習を十分に行うことで、生成器\(G\)から本物データに近いデータが生成できるようになります。

'''
4. Test model
'''
def generate(batch_size=16):
model.eval()
noise = gen_noise(batch_size)
gen = model.G(noise)

return gen

images = generate(batch_size=16)
images = images.squeeze().detach().cpu().numpy()
plt.figure(figsize=(6, 6))
for i, image in enumerate(images):
plt.subplot(4, 4, i+1)
plt.imshow(image, cmap='binary_r')
plt.axis('off')
plt.tight_layout()
plt.show()

これを実行すると、下図のようにな結果が得られ、ノイズデータから画像を生成できることが確認できます。今回はエポック数を20としましたが、更に\(D\)と\(G\)を競い合わせる（学習を進める）ことで、より精度良く画像が生成できることが期待できます。