機械学習・AI

公開日：2020/04/13

深層学習における、数式とコードの境界

深層学習（ディープラーニング）は、数学とプログラミング、両者がシームレスにつながる分野です。本記事では、深層学習で最もベーシックな層である全結合層を題材に、両者の境界を丁寧かつシンプルに解説していきます。全結合層をPythonのクラスとして、順伝播、逆伝播をメソッドとして実装します。
TensorFlowやPyTorchなどのフレームワークを使えばこれらの知識がなくても深層学習の実装はある程度可能なのですが、背景の仕組みについて想像をめぐらし、より深い考察をするためには数学とプログラミングの境界に関する知識と経験があった方が望ましいです。

1 順伝播の数式
2 順伝播をコードで実装する
3 逆伝播の数式
4 逆伝播をコードで実装する
5 中間層の実装例

順伝播の数式

ニューラルネットワークへの入力を、入力層から出力層に向けて伝播させる処理が順伝播です。順伝播は、ニューラルネットワークを用いて予測する際に行われます。
まずは、順伝播を数式で表しましょう。まずは以下の図のような2つの層の間の接続を考えます。

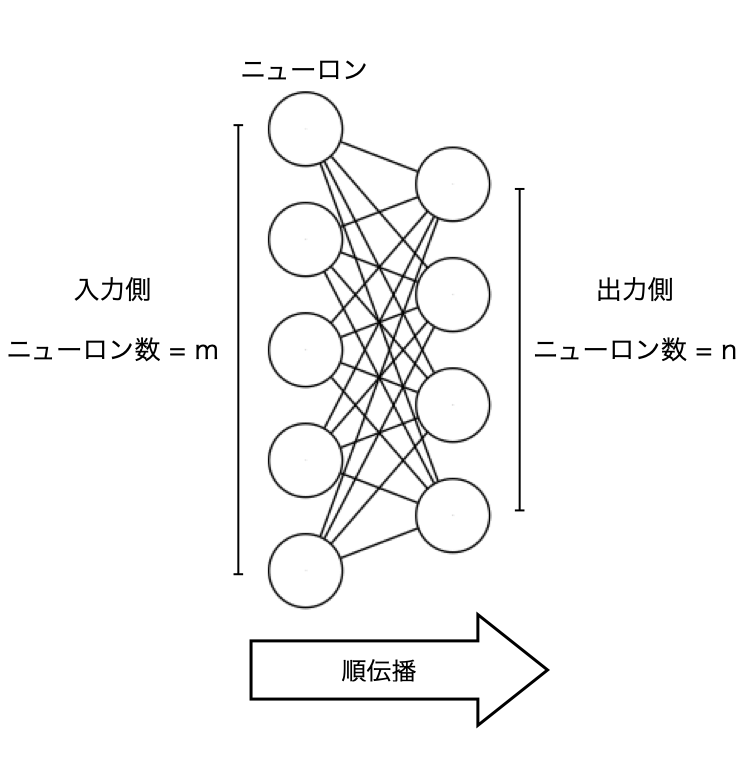
この図において、入力側の層の全てのニューロンは、それぞれ出力側の層の全てのニューロンと接続されています。それでは、ここからは出力側の層に注目しましょう。出力側の層のニューロンへのそれぞれの入力には重みをかけます。重みの数は入力の数と等しいので、入力側の層のニューロン数を\( 𝑚 \)とすると、出力側の層のニューロンは1つあたり\( 𝑚 \)個の重みを持つことになります。出力側の層のニューロン数\( 𝑛 \)とすると、出力側の層には合計\( 𝑚×𝑛 \)個の重みが存在することになります。
このような重みですが、例えば入力側の層の1番目のニューロンから、出力側の層の1番目のニューロンへの入力の重みは \(𝑤_{11} \)と表します。このような重みは、以下のような\( 𝑚×𝑛 \)の行列\( 𝑊 \)に全て格納されます。

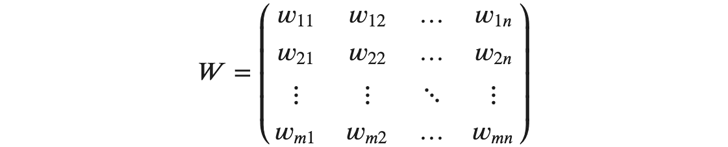
また、出力側の層への入力（=入力側の層の出力）を、とりあえず以下のようにベクトル\( 𝑥⃗ \)で表します。

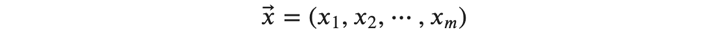
また、バイアス\( 𝑏⃗\) も以下のようにベクトルで表記します。

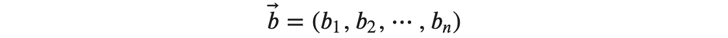
これらを使って、\( 𝑢⃗ \) を次のように表します。

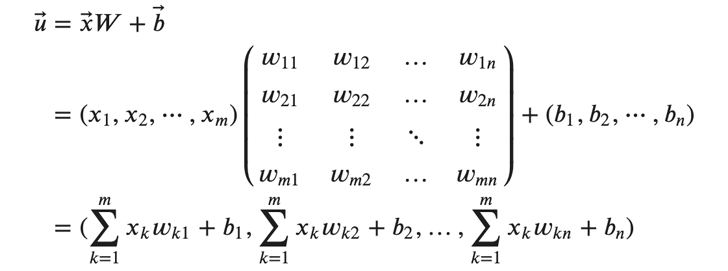
\( 𝑢⃗\) の各要素は、重みと入力の積の総和にバイアスを足したものになっています。

次に、活性化関数を使用します。ベクトル\( 𝑢⃗ \) の各要素を活性化関数 \( 𝑓 \) に入れて処理し、出力を表すベクトル\( 𝑦⃗ \) を得ることができます。

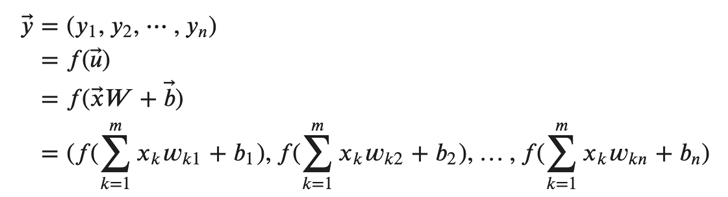
ここまでで、入出力をベクトルとした上でですが順伝播を数式で表すことができました。

順伝播をコードで実装する

先ほどの順伝播の式において、入出力はベクトルでした。この場合、一度に一つの入力しか扱えないためミニバッチ法に対応できません。ミニバッチ法に対応するためには、入出力を行列に拡張する必要があります。
この場合、行列の各行が、バッチ内の各サンプルを表すことになります。入力を行列\( 𝑋 \) 、出力を行列\( 𝑌 \) とすると、それぞれの行列は以下のように表されます。

ここで、\( ℎ \)はバッチサイズです。
また、バイアスはバッチ内で全て同じ値をとるため、以下のようにベクトルを縦方向に引き伸ばした行列\( 𝐵 \)で表すことができます。

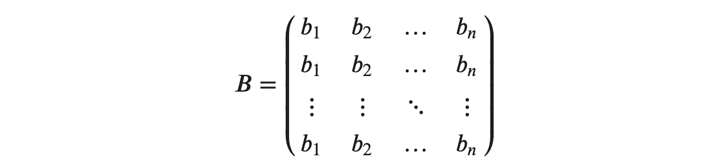
これらの行列を用いて、以前に解説した（式1）（式2）は以下のように拡張されます。

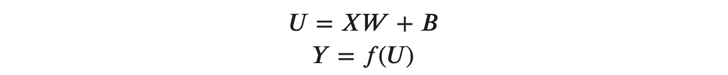
それでは、これらの式の各要素を見ていきましょう。

（式1）と（式2）が、バッチ対応のため縦方向に拡張されています。このように行列で表すことさえできれば、あとは簡単にコードに落とし込むことができます。
（式3）は、以下のようにPythonのコードとして実装されます。 np.dotは数値計算ライブラリNumPyのdot関数ですが、行列積を計算するのに用いられます。

u = np.dot(x, w) + b  # x: 入力の行列 w: 重みの行列 b: バイアスのベクトル
y = f(u)  # y: 出力の行列  f: 活性関数

バイアスbはベクトルですが、これはNumPyのブロードキャスト機能により縦方向に引き延ばされるので、実質行列として扱われます。
順伝播を実装可能な数式で表し、コードに落とし込むことができました。

逆伝播の数式

逆伝播では、出力と正解の誤差を入力に向かって遡らせて、各パラメータ（重みとバイアス）の勾配を求めます。求めた勾配をもとにパラメータを更新することで、学習が行われます。
それでは、以下の順伝播の式から始めましょう。

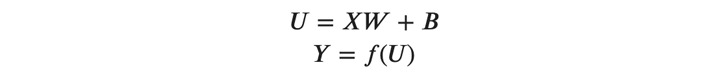
ここで、以下のように\( 𝑈 \)の各要素に注目します。

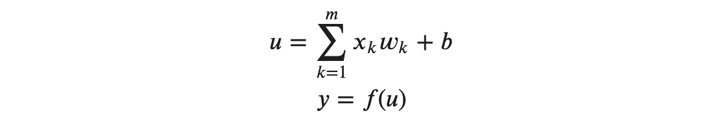
上記の式では、層内の個々のニューロンを識別するための添字、及びバッチを表す添字は省略されています。
ここで、重みの勾配、すなわち誤差の重みによる偏微分を考えます。

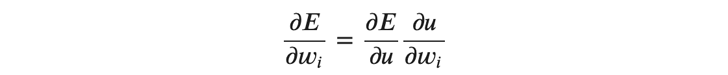
\(𝑤_𝑖 \)は（式4）の総和の記号の中のある重みで、 \(1≤𝑖≤𝑚 \)となります。
ここで、右辺の\( \frac{∂𝐸}{∂𝑢} \)ですが、以下のように\( 𝛿 \)を使って表されます。

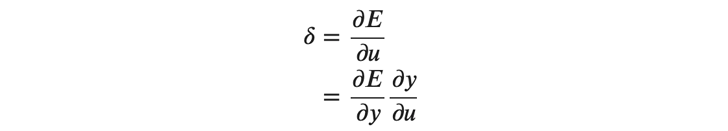
上記のように、 \(𝛿 \)は連鎖律を使って\( \frac{∂𝐸}{∂𝑦} \)と\(\frac{∂𝑦}{∂𝑢} \)に分解することができます。
\(\frac{∂𝐸}{∂𝑦}\) は、最も出力に近い出力層の場合は誤差関数の\( 𝑦 \)による偏微分により、入力層と出力層の間にある中間層の場合は出力側からの伝播により得ることができます。
また、 \(\frac{∂𝑦}{∂𝑢}\) は活性化関数を偏微分して得ることができます。

次に（式5）における \(\frac{∂𝑢}{∂𝑤_𝑖}\) ですが、以下のように偏微分することで得ることができます。

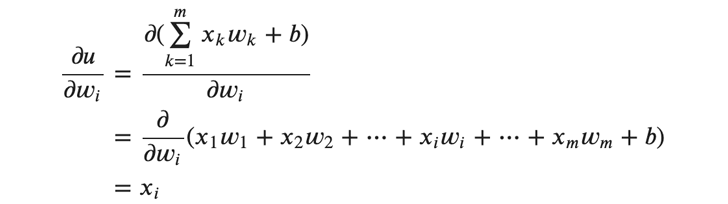
ここで、（式5）（式6）（式7）により、重みの勾配を以下の通りに表すことができます。

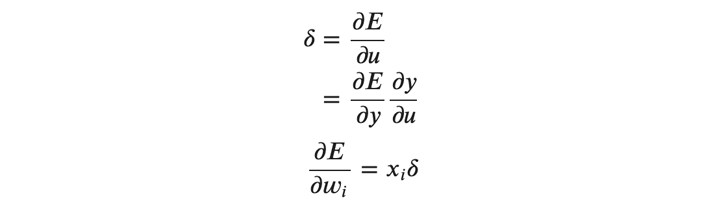
バイアスの勾配ですが、\( 𝑢 \)を\( 𝑏 \)で偏微分すると1になるので、あとは上記と同様にして次のように求めることができます。

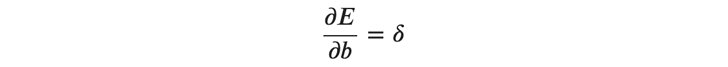
最後に、入力\( 𝑥_𝑖 \)の勾配を求めます。\( 𝑥_𝑖 \)は層内の全てのニューロンに影響を与えるので、連鎖律を層内の全てのニューロンに拡張する必要があります。
入力の勾配は、ニューロン数を\( 𝑛\) として以下のように求めることができます。

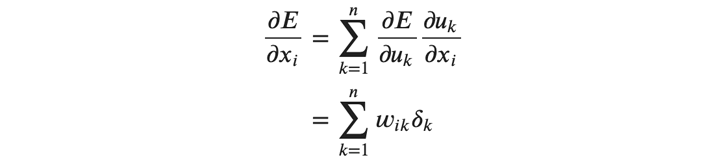
ここで、添字の\( 𝑘 \)は層内の各ニューロンを表します。
この入力の勾配ですが、1つ入力側の層に渡されて、そこで\( 𝛿 \)を求めるために使用されます。

逆伝播をコードで実装する

逆伝播の場合も、ミニバッチ法に対応するために行列で数式を表す必要があります。
以下の、要素ごとの逆伝播の式を行列に拡張します。

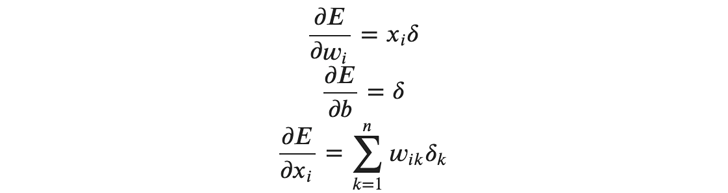
まずは、重みの勾配を行列で表します。重みの勾配はバッチごとに計算する必要があります。
バッチ全体の誤差を\( 𝐸 \)として、重みの勾配を次のように求めます。

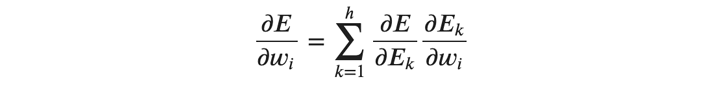
ここで\( ℎ \)はバッチサイズ、\( 𝐸_𝑘 \)はバッチ内のサンプルごとの誤差です。
また、以下に示すようにサンプルごとの誤差の総和がバッチの誤差となります。

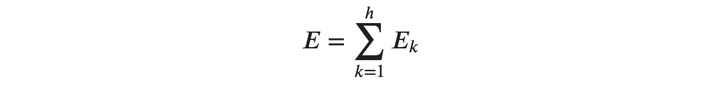
また、（式9）において、

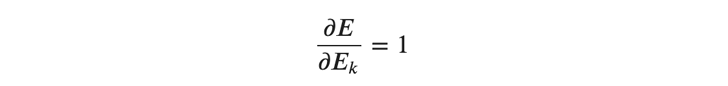
となるので、あるバッチにおける重みの勾配は以下のように表すことができます。

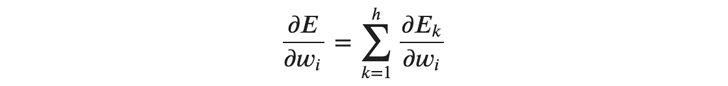
このように、あるバッチの勾配は各サンプルの勾配の総和により求めることができます。
そして、これは行列演算を用いて一度に計算することができます。以下に示すように、行列 \( 𝑋 \)を転置したものと、 \( 𝛿 \)の行列 \(Δ \) の行列積により、バッチ内での総和をとることができます。

行列 \( \frac{∂𝐸}{∂𝑊} \) の各要素は、（式8）で表されるサンプルごとの勾配の総和になっています。

次にバイアスの勾配ですが、これもサンプルごとの勾配の総和により求めることができます。バイアスの勾配はバッチ内で全て同じ値をとるため、以下のように横ベクトルを縦方向に引き伸ばした行列で表すことができます。

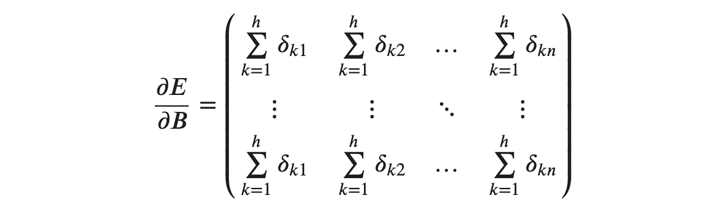
最後に入力の勾配ですが、これはバッチ内で総和をとる必要はありません。その代わり、各サンプル、各入力ごとに重みと\( 𝛿 \) の積の総和を計算します。これは\( Δ \) と\( 𝑊^𝑇 \) の行列積で求めることができます。

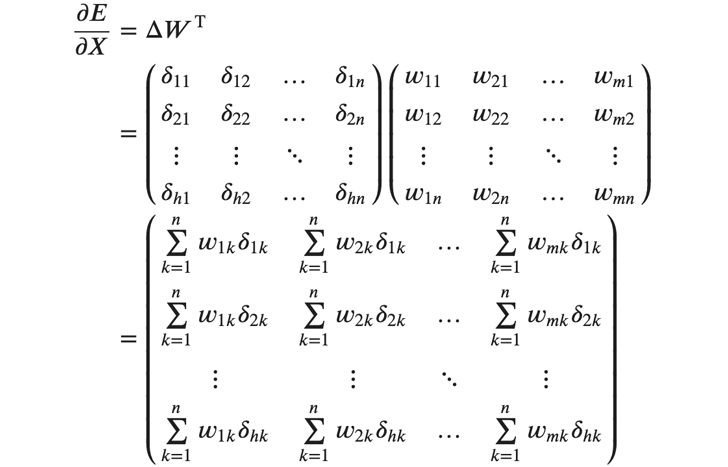
各要素は、層内のニューロンで総和をとったものになります。
要素を行列に拡張することで、逆伝播がミニバッチ法に対応できるようになりました。

以上ををコードで実装しますが、次のようにNumPyのdot関数やsum関数を使えば、シンプルなコードで実装することができます。

# x: 入力の行列  w: 重みの行列  delta: δの行列
grad_w = np.dot(x.T, delta)  # wの勾配
grad_b = np.sum(delta, axis=0)  # bの勾配
grad_x = np.dot(delta, w.T)  # xの勾配

バイアスの勾配は、axis=0、すなわち縦方向（バッチ内）で総和をとることにより求めています。この場合grad_bの行数は1になりますが、必要に応じてブロードキャストにより引き伸ばして使います。
逆伝播に必要な数式を、コードに落とし込むことができました。

中間層の実装例

これまでに解説した順伝播と逆伝播のコードをもとに、中間層をクラスとして実装します。以下は中間層の実装例です。初期化のための__init__メソッド、順伝播のforwardメソッド、逆伝播のbackwardメソッド、パラメータ更新用のupdateメソッドが含まれます。

class MiddleLayer(BaseLayer):
    def __init__(self, n_in, n):
        self.w = np.random.randn(n_in, n) * np.sqrt(2/n_in)  # Heの初期値
        self.b = np.zeros(n)
 
    def forward(self, x):
        self.x = x
        self.u = np.dot(x, self.w) + self.b
        self.y = np.where(self.u <= 0, 0, self.u) # ReLU
 
    def backward(self, grad_y):
        delta = grad_y * np.where(self.u <= 0, 0, 1)  # ReLUの微分
 
        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)
        self.grad_x = np.dot(delta, self.w.T) 
 
    def update(self, eta):
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b

n_inは入力の数、nはこの層のニューロン数です。
backwardメソッドにおいて、引数のgrad_yは出力側の層から伝播してきた出力の勾配です。この層で各勾配を計算し、updateメソッドでパラメータを更新します。
以上のように、深層学習における層はシンプルなコードでクラスとして実装することができます。数式からコードへのスムーズな移行が、フレームワークを使わない深層学習の実装のキーになります。
より発展した内容や、より丁寧な解説について知りたい方は、拙著「はじめてのディープラーニング」「はじめてのディープラーニング2」（SBクリエイティブ）をぜひ参考にしてください。「はじめてのディープラーニング」はCNNまでを、「はじめてのディープラーニング2」はRNN、LSTM、GRU、VAE、GANまでを扱います。

我妻幸長

「ヒトとAIの共生」がミッションの会社、SAI-Lab株式会社の代表取締役。AI関連の教育と研究開発に従事。東北大学大学院理学研究科修了。理学博士（物理学）。
オンライン教育プラットフォームUdemyで、3.5万人以上にAIを教える人気講師。
著書に、「はじめてのディープラーニング」「はじめてのディープラーニング2」（SBクリエイティブ）、「Pythonで動かして学ぶ！あたらしい数学の教科書」（翔泳社）。